题解
剑指 Offer 51. 数组中的逆序对
思路一:两层循环,$O(N^2)$
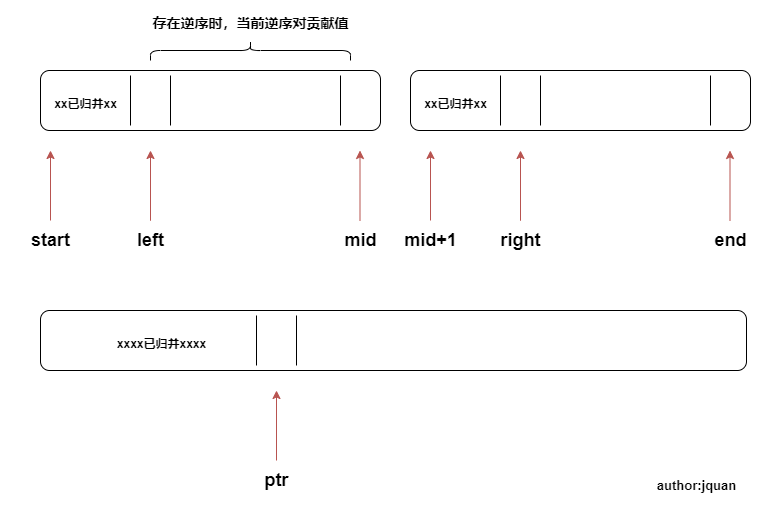
思路二:基于归并排序的过程,累加逆序对数量;$O(logN)$
- 理解归并过程中,逆序对贡献度的计算方法
- 归并算法
package SwordOf.DivideAndConquerAlgorithm;
import org.junit.Test;
public class ReversePairs {
public int reversePairs(int[] nums) {
if(nums.length==0 || nums==null) return 0;
return reverseProcess(nums,0,nums.length-1);
}
private int reverseProcess(int[] nums,int start,int end){
if(start == end) return 0;
int mid = (start+end)/2;
int left = start,right=mid+1;//分为[left,mid][mid+1,end]
int res = reverseProcess(nums,start,mid)+reverseProcess(nums,mid+1,end);
int[] temArr = new int[end-start+1];
int ptr=0,reverseContribute=0;
while(left<=mid && right<=end){
if(nums[right]<nums[left]){
reverseContribute = mid-left+1;
res+= reverseContribute;
temArr[ptr++] = nums[right++];
}else if(nums[right]>nums[left]){
temArr[ptr++] = nums[left++];
}else{
temArr[ptr++] = nums[left++];
}
}
while(left <= mid) temArr[ptr++] = nums[left++];
while(right<= end) temArr[ptr++] = nums[right++];
for(int i=start;i<=end;i++){
nums[i] = temArr[i-start];
}
return res;
}
@Test
public void test(){
int[] nums = new int[]{7,6,5,4};
int res = reversePairs(nums);
System.out.println(res);
}
}
剑指 Offer 49. 丑数
思路
- 每个丑数一定可以由较小的丑数x2,或者x3,或者x5得到。
- 如果我们求的是无穷多个丑数,那么每个丑数,都会生成3个对应较大的丑数,每个丑数都有3次机会
- 我们用3个指针表示每个丑数生成较大丑数的机会。ptrI 表示当前 用自身值乘以I生成新丑数的丑数下标。显然,3个指针都是从1开始递增,每个生成丑数都有3次机会
- 做题的话理解到上面就可以了,但深究还有1个细节:2,3,5是互质的。所以每个数乘以2,乘以3,乘以5,得到的数不会相同。并且,对于任意的$x,y,z \in N+, 2^x,3^y,5^z$两两之间不可能相等,易证。
class Solution {
public int nthUglyNumber(int n) {
int [] dp = new int[n+1];
dp[1]=1;
//ptrI表示上一个还未使用质因子I求新丑数的下标
int ptr2=1, ptr3=1,ptr5=1;
for(int i=2;i<=n;i++){
dp[i] = minOf3(dp[ptr2]*2,dp[ptr3]*3,dp[ptr5]*5);
if(dp[i]==dp[ptr2]*2) ptr2++;
if(dp[i]==dp[ptr3]*3) ptr3++;
if(dp[i]==dp[ptr5]*5) ptr5++;
}
return dp[n];
}
private int minOf3(int a,int b, int c){
return Math.min(Math.min(a,b),c);
}
}
剑指 Offer 38. 字符串的排列
好题(思想和代码的锻炼价值都很高),本题的最优解基于掌握:「31. 下一个排列的官方题解」
为了穷举所有排列,每次都通过nextPermutation来判断是否存在下一个排列(时间复杂度O(n)), 全部排列由$n!$可能,所以这是最快的解法,时间复杂度 $O(n*(n!))$.代码的关键在于nextPermutation。简单回顾一下
-
因为要穷举全部,初始状态对序列数组排序,呈升序状态。
-
寻找符合要求的a[i], 再寻找符合要求的a[j]
- 能找到i, 说明至少存在nextPermutation,否则return false
-
找到a[i],a[j]后交换,此时a[i+1]....a[len-1] 一定是降序的
-
利用a[i+1]....a[len-1] 是降序的性质,再O(n)内将其排序为升序。得到想要的nextPermutation状态。
-
寻找a[i]a[j]过程中high level 层面的思想就是,找到两个数,一个在左边一个在右边,右边的数比左边的数大,交换他们得到的新序列比原来更大。我们希望还变大的幅度尽可能小。这就要求
- 左边的数尽可能靠右
- 右边的数尽可能小
package SwordOf.Search.Recurse;
import org.junit.Test;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Permutation {
public String[] permutation(String s) {
char[] chArr = s.toCharArray();
List<String> res = new ArrayList<>();
Arrays.sort(chArr);
res.add(String.valueOf(chArr));
while (nextPermutation(chArr)) {
res.add(String.valueOf(chArr));
}
return res.toArray(new String[res.size()]);
}
boolean nextPermutation(char[] arr) {
boolean findRes = false;
//找a[i]
int i = arr.length - 2;
while (i >= 0) {
if (arr[i] < arr[i + 1]) {
findRes = true;
break;
}
i--;
}
if (findRes) {
int j = arr.length - 1;
//上面保证了这里至少能找到一个j
while (j > i) {
if (arr[j] > arr[i]) break;
j--;
}
swap(arr, i, j);
//将a[i+1],...,a[len-1]这一段重排是升序。由于当前状态是降序,直接做交换可以在O(n)时间内完成
reverse(arr, i + 1, arr.length - 1);
}
return findRes;
}
private void swap(char[] arr, int left, int right) {
char temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
private void reverse(char[] arr, int start, int end) {
while (end > start) {
swap(arr, start, end);
start ++;
end --;
}
}
@Test
public void test(){
String s = "mdpesmo";
String [] res = permutation(s);
System.out.println(Arrays.toString(res));
}
}
剑指 Offer 37. 序列化二叉树
官方题解写的实在不咋地,而且不规范,比如方法一 java题解中, str += str.valueOf(root.val) + "," 应为str += String.valueOf(root.val) + "," ,不知道题解是怎么通过的,改成这样也能通过。valueOf 是String 的静态方法
大致思路和细节:
- 对于空孩子,用一个标识符来标识,比如"$", 这样只需要对树做一次遍历就可以缺定树的构成(满二叉树,一个萝卜一个坑)。
- 每个结点值可能是负数,以及几位数不缺定,因为要序列化为字符串,所以每个值都需要加入一个分隔标识符,方便后面的反序列化,比如“,”
- 还有个小细节,序列化字符串最后是以“,”结尾,用split分割后String数组最后应该有一个空元素“”, 这里不用管。因为在遇到之前,递归建树已经终止了。
附上我的题解,个人觉得更加简洁易懂
public class Codec {
private int pos = -1;
// Encodes a tree to a single st5ring.
public String serialize(TreeNode root) {
String serializeOrder = "";
if (root == null) {
serializeOrder += "$,";
return serializeOrder;
}
serializeOrder += root.val+",";
serializeOrder += serialize(root.left);
serializeOrder += serialize(root.right);
return serializeOrder;
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
String[] strArr = data.split(",");
return deserializeSup(strArr);
}
public TreeNode deserializeSup(String[] dataArr) {
pos++;
String cur = dataArr[pos];
TreeNode node;
if (!cur.equals("$")){
node = new TreeNode(Integer.valueOf(cur));
node.left = deserializeSup(dataArr);
node.right = deserializeSup(dataArr);
}else return null;
return node;
}
}
5. 最长回文子串
动态规划解法
- 动态规划思路:利用动态规划的思想,每一个回文串都是由更短的回文串组成的。(原问题可以通过一步操作,变成规模更小的子问题来解决)。
- 符号和数学定义:
- s[i,j] 表示s的一个字串,从i开始,j结束
- $P(i,j)表示s[i,j]是否是回文串,P(i,j)={true,false)$
- 转移方程:$P(i,j)=P(i+1,j-1)^(S_i == S_j)$
- 边界条件:$P(i,i)=true ; P(i,i+1)=(S_i == S_{i+1})$
- 注意:动态规划本质是查表法,程序执行过程不断填表,既从短串到长串的过程;
public class SoHuiWengCuan {
public String longestPalindrome(String s) {
int strlen = s.length();
if (strlen < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i..j] 是否是回文串
boolean[][] dp = new boolean[strlen][strlen];
// 初始化:所有长度为 1 的子串都是回文串
for (int i = 0; i < strlen; i++) {
dp[i][i] = true;
}
char[] charArray = s.toCharArray();
// 递推开始
// 先枚举子串长度
for (int subL = 2; subL <= strlen; subL++) {
// 枚举左边界,左边界的上限设置可以宽松一些
for (int i = 0; i < strlen; i++) {
// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
int j = subL + i - 1;
// 如果右边界越界,就可以退出当前循环
if (j >= strlen) {
break;
}
if (charArray[i] != charArray[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) { // 边界情况:既 aba,aa,a 情况;
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substring(begin, begin + maxLen);
}
}
复杂度
- 时间复杂度:$O(n^2)$;动态规划状态总数$O(n^2)$ , 求解每一个状态%$O(1)$时间
- 空间复杂度:$O(n^2)$




评论
1 / 1