题目描述

题目链接

样例

输入：
4 5
1 2
2 4
3 4
4 6
输出：
2

分析：

• 本题核心和易错的点在于，关于状态的定义，导致初始化得不同，以及求解的不同：

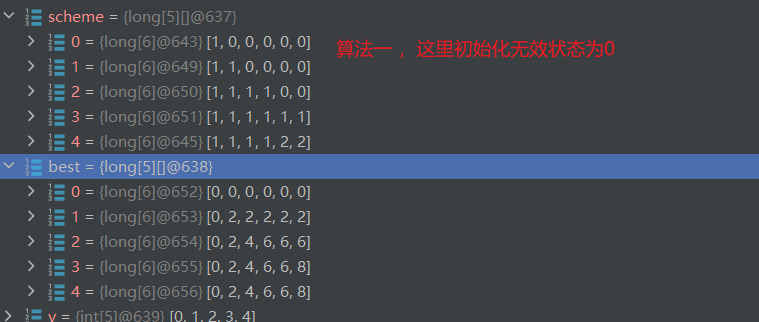
• 一)算法一

• 定义

  • best[i] [j]: 表示从前i个物品中选择，**体积就是**j的价值
  • scheme[i] [j] 表示表示从前i个物品种选择**体积就是**j的最大价值对应方案数

• 初始化：

  • best[0] [0]=0 其他，其他 i,j, best[i] [j] = - INF ;
  • scheme[0] [0] = 1; // 这也就解释了，为什么图1scheme中那么多中间非法状态
  • 只能是scheme[0] [0]=1 ，scheme[0] [1-V]=0或者负无穷； 其他状态要和 best 状态保持一致，是非法的，因为是best的约束是恰好填满，其他是非法状态~

• 求最后解时

  • 累加 scheme[N] [0->V]

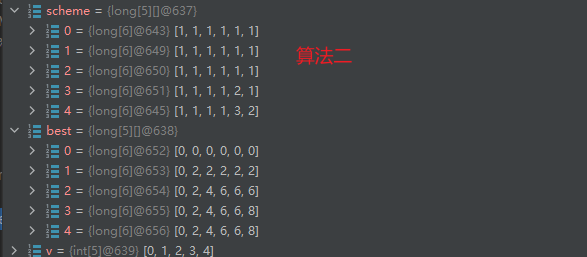
• 二)算法二

• 定义

  • best[i] [j]: 表示从前i个物品中选择，体积**不大于**j的价值
  • scheme[i] [j] 表示表示从前i个物品种选择体积不大于j的最大价值对应方案数

• 初始化：

  • best[i] [j]=0 ,i , j 任意 ;
  • 必须scheme[0] [0-V] = 1; // （都必须填1）
  • scheme[0-N] [0] = 1; // 可以不显示初始化，只要保证scheme[0] [0]=1, scheme[0-N] [0]在代码中会被填为1；

• 求最后解时

  • 直接输出 scheme[N] [V] , 所有状态的解已经递推并保存在这里

package codefortopic.PackPro;

import java.lang.reflect.Array;
import java.util.Arrays;
import java.util.Scanner;

public class SchemeNum {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();
        int V = sc.nextInt();
        sc.nextLine();
        long[][] scheme = new long[N+1][V+1];
        long[][] best = new long[N+1][V+1];
        int[] v = new int[N+1];
        int[] w = new int[N+1];
        int P = (int) (1e9+7);

        for(int i=1;i<=N;i++){
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
            if(i!=N)
            sc.nextLine();
        }
        //初始化一 算法一
        /*for(int i=0;i<=N;i++){
            scheme[i][0] = 1; //当v为0，不管考虑几件物品，best的解是什么都不选，所以scheme解为1
        }*/
       /* //初始化二 算法一
        scheme[0][0] = 1;*/


        //初始化三 算法二
        for(int j=0;j<=V;j++){
            scheme[0][j] = 1;
        }
        for(int i=0;i<=N;i++){ //当v为0，不管考虑几件物品，best的解是什么都不选，所以scheme解为1
            scheme[i][0] = 1;
        }

        for(int i=1;i<=N;i++){
            for(int j = 0; j<=V; j++){
                if(j>=v[i])
                    best[i][j] = Math.max(best[i-1][j],best[i-1][j-v[i]]+w[i]);
                else best[i][j] = best[i-1][j];

                scheme[i][j] = 0;
                if(best[i][j] == best[i-1][j]){
                    scheme[i][j] = scheme[i-1][j];
                }
                if(j>=v[i] && best[i][j] == best[i-1][j-v[i]]+w[i]){
                    scheme[i][j] += scheme[i-1][j-v[i]];
                }
                if(scheme[i][j]>=P) scheme[i][j] %= P;
            }
        }


        //算法一需要累加
     /*   long ans = 0;
        for(int j=0;j<=V;j++){ //枚举的是v， 而不能是物品件数
            if(best[N][j] == best[N][V]){
                ans += scheme[N][j];
                if(ans>P) ans %=P;
            }
        }
*/

        //算法一
//        System.out.println(ans);
        //算法二
        System.out.println(scheme[N][V]);
    }
}